Inhoud

• Stappen
• Advies

Variantie meet de spreiding van de dataset. Het is erg handig bij het bouwen van statistische modellen: lage variantie kan een indicatie zijn dat u willekeurige fouten of ruis beschrijft in plaats van de onderliggende relatie in de gegevens. Met dit artikel leert wikiHow je hoe je variantie kunt berekenen.

Stappen

Methode 1 van 2: Bereken de variantie van een steekproef

1. 

   Schrijf uw voorbeeldgegevensset. In de meeste gevallen hebben statistici alleen informatie over een steekproef of een deel van de populatie die ze bestuderen. In plaats van een algemene analyse uit te voeren van "de kosten van alle auto's in Duitsland", zou een statisticus bijvoorbeeld de kosten van een willekeurige steekproef van een paar duizend auto's kunnen berekenen. De statisticus kan deze steekproef gebruiken om een ​​goede schatting te krijgen van de kosten van auto's in Duitsland. Het is echter waarschijnlijker dat het niet exact overeenkomt met de werkelijke cijfers.
   • Bijvoorbeeld: Bij het analyseren van het aantal muffins dat per dag in een coffeeshop wordt verkocht, nam u een willekeurig zesdaags monster en kreeg u de volgende resultaten: 38, 37, 36, 28, 18, 14, 12, 11, 10,7, 9,9. Dit is een steekproef, geen populatie, omdat u niet beschikt over gegevens voor elke dag dat de winkel open is.
   • Als elke Datapunten in de master, ga naar de onderstaande methode.

2. 

   
   
   Schrijf de steekproefvariantieformule op. De variantie van een dataset geeft de mate van spreiding van de datapunten aan. Hoe dichter de variantie bij nul is, hoe dichter de gegevenspunten zijn gegroepeerd. Gebruik de volgende formule om de variantie te berekenen wanneer u met voorbeeldgegevenssets werkt:
   • = /_{(n - 1)}
   • is de variantie. Variantie wordt altijd berekend in kwadraateenheden.
   • vertegenwoordigt een waarde in uw dataset.
   • ∑, wat "som" betekent, vertelt u om de volgende parameters voor elke waarde te berekenen en ze vervolgens bij elkaar op te tellen.
   • x̅ is het gemiddelde van de steekproef.
   • n is het aantal datapunten.

3. 

   
   
   Bereken het gemiddelde van de steekproef. Het symbool x̅ of "x-horizontaal" wordt gebruikt om het gemiddelde van het monster aan te geven. Bereken zoals elk gemiddelde: tel alle gegevenspunten bij elkaar op en deel ze door het aantal punten.
   • Bijvoorbeeld: Tel eerst uw gegevenspunten op: 17 + 15 + 23 + 7 + 9 + 13 = 84
     Deel vervolgens het resultaat door het aantal gegevenspunten, in dit geval zes: 84 ÷ 6 = 14.
     Steekproefgemiddelde = x̅ = 14.
   • U kunt het gemiddelde zien als het "middelpunt" van de gegevens. Als de gegevens rond het gemiddelde zijn gecentreerd, is de variantie laag. Als ze ver van het gemiddelde zijn verspreid, is de variantie groot.

4. 

   
   
   Trek het gemiddelde van elk gegevenspunt af. Dit is het moment om - x̅ te berekenen, waar elk punt in uw dataset is. Elk resultaat geeft de afwijking aan van het gemiddelde van elk corresponderend punt, of simpel gezegd, de afstand ervan tot het gemiddelde.
   • Bijvoorbeeld:
     - x̅ = 17 - 14 = 3
     - x̅ = 15 - 14 = 1
     - x̅ = 23 - 14 = 9
     - x̅ = 7 - 14 = -7
     - x̅ = 9 - 14 = -5
     - x̅ = 13 - 14 = -1
   • Het is heel gemakkelijk om uw berekeningen te controleren, want de resultaten moeten opgeteld nul zijn, dat komt omdat door het gemiddelde van het gemiddelde de negatieve resultaten (de afstand van het gemiddelde tot kleine getallen). positieve resultaten (afstand van gemiddelde tot grotere getallen) worden volledig geëlimineerd.

5. 

   Maak alle resultaten vierkant. Zoals hierboven opgemerkt, heeft de huidige deviatielijst (- x sum) een som van 0. Dat betekent dat de "gemiddelde deviatie" ook altijd nul zal zijn en er kan niets gezegd worden over de spreiding van de gegevens. Om dit probleem op te lossen, zoeken we het kwadraat van elke afwijking. Dankzij dat zijn het allemaal positieve getallen, negatieve waarden en positieve waarden heffen elkaar niet langer op en geven de som nul.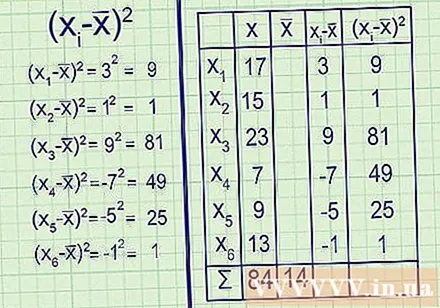
   • Bijvoorbeeld:
     (- x̅)
     - x̅)
     9 = 81
     (-7) = 49
     (-5) = 25
     (-1) = 1
   • U heeft nu (- x̅) voor elk gegevenspunt in de steekproef.

6. 

   Zoek de som van de gekwadrateerde waarden. Dit is het moment om de volledige teller van de formule te berekenen: ∑. De grote cyclo, ∑, vereist dat u voor elke waarde de volgende elementwaarde toevoegt. U hebt (- x̅) berekend voor elke waarde in de steekproef, dus u hoeft alleen maar de resultaten bij elkaar op te tellen.
   • Bijvoorbeeld: 9 + 1 + 81 + 49 + 25 + 1 = 166.

7. 

   Deel door n - 1, waarbij n het aantal gegevenspunten is. Lang geleden, toen de steekproefvariantie werd berekend, werden statistici alleen gedeeld door n. Die deling geeft je het gemiddelde van de kwadraatafwijking, die exact overeenkomt met de variantie van die steekproef. Houd er echter rekening mee dat de steekproef slechts een schatting is van een grotere populatie. Als je nog een willekeurige steekproef neemt en dezelfde berekening uitvoert, krijg je een ander resultaat. Het blijkt dat delen door n -1 in plaats van n je een betere schatting geeft van de variantie van een grotere populatie - waar je echt om geeft. Deze correctie is zo gewoon dat het nu de geaccepteerde definitie van steekproefvariantie is.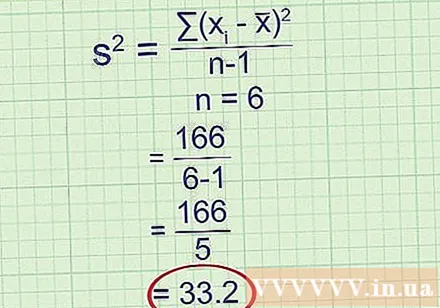
   • Bijvoorbeeld: Er zijn zes gegevenspunten in de steekproef, dus n = 6.
     Steekproefvariantie = 33,2

8. 

   Begrijp variantie en standaarddeviatie. Merk op dat, aangezien de formule machten bevat, de variantie wordt gemeten in het kwadraat van de eenheden van de oorspronkelijke gegevens. Dit is visueel verwarrend. In plaats daarvan is de standaarddeviatie vaak erg handig. Maar het heeft geen zin om moeite te verspillen, want de standaarddeviatie wordt bepaald door de vierkantswortel van de variantie. Daarom is de steekproefvariantie in termen geschreven, en de standaarddeviatie van een steekproef is.
   • De standaarddeviatie van de bovenstaande steekproef = s = √33,2 = 5,76.
   advertentie

Methode 2 van 2: Bereken de variantie van een populatie

1. 

   Te beginnen met de stamgegevensset. De term "populatie" wordt gebruikt om naar alle relevante waarnemingen te verwijzen. Als u bijvoorbeeld onderzoek doet naar de leeftijd van de inwoners van Hanoi, omvat uw totale populatie de leeftijden van alle personen die in Hanoi wonen. Gewoonlijk zou u een spreadsheet maken voor een grote dataset zoals deze, maar hier is een kleinere voorbeelddataset:
   • Bijvoorbeeld: In de kamer van een aquarium zijn precies zes aquaria. Deze zes tanks bevatten de volgende aantallen vissen:
     
     
     
     
     
     

2. 

   Schrijf de formule op voor algemene variantie. Omdat een populatie alle gegevens bevat die we nodig hebben, geeft deze formule ons de exacte variantie van de populatie. Om het te onderscheiden van de steekproefvariantie (die slechts een schatting is), gebruiken statistici andere variabelen:
   • σ = /_n
   • σ = steekproefvariantie. Dit is de normaal vierkante worst. Variantie wordt gemeten in vierkante eenheden.
   • vertegenwoordigt een element in uw dataset.
   • Het element in ∑ wordt voor elke waarde berekend en vervolgens opgeteld.
   • μ is het algemene gemiddelde.
   • n is het aantal datapunten in de populatie.

3. 

   Zoek het gemiddelde van de populatie. Bij het analyseren van een populatie stelt het symbool μ ("mu") het rekenkundig gemiddelde voor. Om het gemiddelde te vinden, telt u alle gegevenspunten op en deelt u deze vervolgens door het aantal punten.
   • Je kunt betekenen als "gemiddeld" beschouwen, maar wees voorzichtig, want het woord heeft veel wiskundige definities.
   • Bijvoorbeeld: gemiddelde waarde = μ = = 10,5

4. 

   Trek het gemiddelde van elk gegevenspunt af. Gegevenspunten dichter bij het gemiddelde hebben een verschil dichter bij nul. Herhaal het aftrekprobleem voor alle gegevenspunten en u zult waarschijnlijk de spreiding van de gegevens gaan voelen.
   • Bijvoorbeeld:
     - μ = 5 – 10,5 = -5,5
     - μ = 5 – 10,5 = -5,5
     - μ = 8 – 10,5 = -2,5
     - μ = 12 - 10., = 1,5
     - μ = 15 – 10,5 = 4,5
     - μ = 18 – 10,5 = 7,5

5. 

   Maak elk bord vierkant. Op dit punt zullen sommige resultaten die zijn verkregen uit de vorige stap negatief zijn en sommige zullen positief zijn.Als u de gegevens op een isomorfe lijn visualiseert, vertegenwoordigen deze twee items de getallen links en rechts van het gemiddelde. Dit heeft geen zin om de variantie te berekenen, aangezien deze twee groepen elkaar opheffen. Zet ze in plaats daarvan allemaal vierkant zodat ze allemaal positief zijn.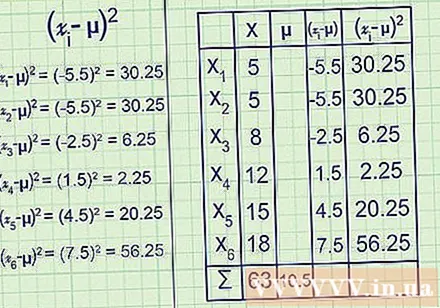
   • Bijvoorbeeld:
     (- μ) voor elke waarde van ik loopt van 1 tot 6:
     (-5,5) = 30,25
     (-5,5) = 30,25
     (-2,5) = 6,25
     (1,5) = 2,25
     (4,5) = 20,25
     (7,5) = 56,25

6. 

   Vind het gemiddelde van uw resultaten. Je hebt nu een waarde voor elk datapunt, gerelateerd (niet direct) aan hoe ver dat datapunt verwijderd is van het gemiddelde. Gemiddeld door ze bij elkaar op te tellen en te delen door het aantal waarden dat u heeft.
   • Bijvoorbeeld:
     Algemene variantie = 24,25

7. 

   Contact recept. Als u niet zeker weet hoe dit past bij de formule die aan het begin van de methode wordt beschreven, schrijf dan het hele probleem met de hand op en kort niet af: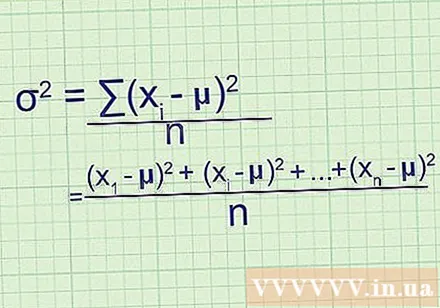
   • Nadat u het verschil met het gemiddelde en het kwadraat hebt gevonden, krijgt u (- μ), (- μ), enzovoort tot (- μ), waar is het laatste gegevenspunt. in de dataset.
   • Om het gemiddelde van deze waarden te vinden, tel ze bij elkaar op en deel ze door n: ((- μ) + (- μ) + ... + (- μ)) / n
   • Na het herschrijven van de teller met sigmoïde notatie, heb je /_n, formule variantie.
   advertentie

Advies

• Omdat de variantie moeilijk te interpreteren is, wordt deze waarde vaak berekend als startpunt voor het vinden van de standaarddeviatie.
• Het gebruik van "n-1" in plaats van "n" in de noemer is een techniek die Bessel-correctie wordt genoemd. De steekproef is slechts een schatting van een volledige populatie, en het gemiddelde van de steekproef heeft een zekere vertekening om bij die schatting te passen. Deze correctie elimineert de bovenstaande bias. Het betreft het feit dat eenmaal n - 1 datapunten zijn opgesomd, het laatste punt n was een constante, omdat alleen bepaalde waarden werden gebruikt om het gemiddelde van de steekproef (x̅) in de variantieformule te berekenen.