Inhoud

• Stappen
• Methode 1 van 3: Deel 1: Het buigpunt bepalen
• Methode 2 van 3: De derivaten van een functie berekenen
• Methode 3 van 3: Deel 3: Vind het buigpunt
• Tips

In differentiaalrekening is een buigpunt een punt op een kromme waarbij de kromming van teken verandert (van plus naar min of van min naar plus). Dit concept wordt gebruikt in de machinebouw, economie en statistiek om significante veranderingen in gegevens te identificeren.

Stappen

Methode 1 van 3: Deel 1: Het buigpunt bepalen

1. 1 Definitie van een concave functie. Het midden van elk akkoord (een segment dat twee punten verbindt) van de grafiek van een concave functie ligt ofwel onder de grafiek of erop.
2. 2 Definitie van een convexe functie. Het midden van elk akkoord (een segment dat twee punten verbindt) van de grafiek van een convexe functie ligt ofwel boven de grafiek of erop.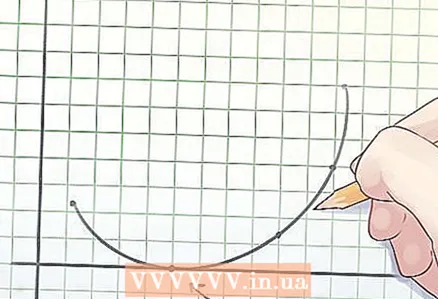
3. 3 Bepaling van de wortels van de functie. De wortel van een functie is de waarde van de variabele "x" waarbij y = 0.
   • Bij het plotten van een functie zijn de wortels de punten waarop de grafiek de x-as kruist.

Methode 2 van 3: De derivaten van een functie berekenen

1. 1 Zoek de eerste afgeleide van de functie. Kijk naar de differentiatieregels in het leerboek; je moet leren hoe je de eerste afgeleiden moet nemen en pas daarna overgaan tot complexere berekeningen. De eerste afgeleiden worden aangeduid met f '(x). Voor uitdrukkingen van de vorm ax ^ p + bx ^ (p 1) + cx + d is de eerste afgeleide: apx ^ (p − 1) + b (p - 1) x ^ (p − 2) + c.
   • Zoek bijvoorbeeld de buigpunten van de functie f (x) = x ^ 3 + 2x -1. De eerste afgeleide van deze functie is:
     
     f ′ (x) = (x ^ 3 + 2x - 1) ′ = (x ^ 3) ′ + (2x) ′ - (1) ′ = 3x ^ 2 + 2 + 0 = 3x2 + 2
2. 2 Zoek de tweede afgeleide van de functie. De tweede afgeleide is de afgeleide van de eerste afgeleide van de oorspronkelijke functie. De tweede afgeleide wordt aangeduid als f ′ ′ (x).
   • In het bovenstaande voorbeeld is de tweede afgeleide:
     
     f ′ ′ (x) = (3x2 + 2) ′ = 2 × 3 × x + 0 = 6x
3. 3 Stel de tweede afgeleide in op nul en los de resulterende vergelijking op. Het resultaat is het verwachte buigpunt.
   • In het bovenstaande voorbeeld ziet uw berekening er als volgt uit:
     
     f ′ ′ (x) = 0
     6x = 0
     x = 0
4. 4 Zoek de derde afgeleide van de functie. Om te controleren of uw resultaat daadwerkelijk een buigpunt is, zoekt u de derde afgeleide, die de afgeleide is van de tweede afgeleide van de oorspronkelijke functie. De derde afgeleide wordt aangeduid als f ′ ′ ′ (x).
   • In het bovenstaande voorbeeld is de derde afgeleide:
     
     f ′ ′ ′ (x) = (6x) ′ = 6

Methode 3 van 3: Deel 3: Vind het buigpunt

1. 1 Bekijk de derde afgeleide. De standaardregel voor het schatten van een buigpunt is dat als de derde afgeleide niet nul is (d.w.z. f ′ ′ ′ (x) ≠ 0), dan is het buigpunt het echte buigpunt. Bekijk de derde afgeleide; als het niet nul is, dan heb je het echte buigpunt gevonden.
   • In het bovenstaande voorbeeld is de derde afgeleide 6, niet 0.Dus je hebt het echte buigpunt gevonden.
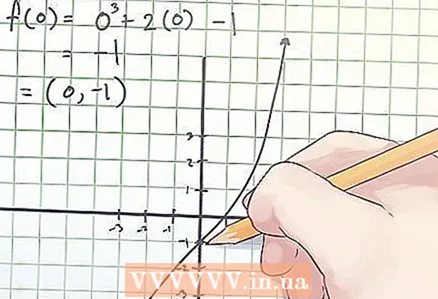
2. 2 Zoek de coördinaten van het buigpunt. De coördinaten van het buigpunt worden aangegeven als (x, f (x)), waarbij x de waarde is van de onafhankelijke variabele "x" op het buigpunt, f (x) de waarde is van de afhankelijke variabele "y" op de buiging punt.
   • In het bovenstaande voorbeeld, bij het gelijkstellen van de tweede afgeleide aan nul, vond je dat x = 0. Dus, om de coördinaten van het buigpunt te bepalen, zoek f (0). Je berekening ziet er als volgt uit:
     
     f (0) = 0 ^ 3 + 2 × 0-1 = -1.
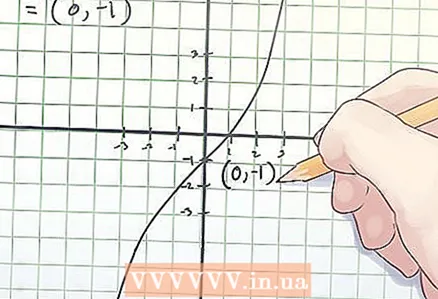3. 3 Schrijf de coördinaten van het buigpunt op. De coördinaten van het buigpunt zijn de gevonden x- en f (x)-waarden.
   • In het bovenstaande voorbeeld ligt het buigpunt op coördinaten (0, -1).

Tips

• De eerste afgeleide van een vrije term (priemgetal) is altijd nul.