Inhoud

• Stappen
• Tips

De rationale functie heeft de vorm y = N (x) / D (x), waarbij N en D polynomen zijn. Om zo'n functie nauwkeurig te plotten, heb je een goede kennis van algebra nodig, inclusief differentiaalberekeningen. Beschouw het volgende voorbeeld: ja = (2x - 6x + 5)/(4x + 2).

Stappen

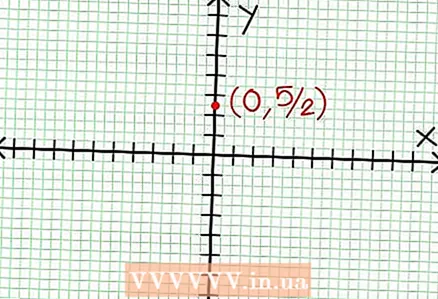1. 1 Zoek het y-snijpunt van de grafiek. Om dit te doen, vervangt u x = 0 in de functie en krijgt u y = 5/2. Het snijpunt van de grafiek met de Y-as heeft dus coördinaten (0, 5/2).Plaats dit punt op het coördinatenvlak.
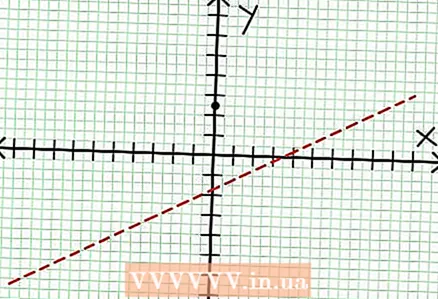2. 2 Zoek de horizontale asymptoten. Deel de teller door de noemer (in een kolom) om het gedrag van "y" te bepalen met waarden van "x" die naar oneindig neigen. In ons voorbeeld is de deling ja = (1/2)x - (7/4) + 17/(8x + 4). Voor grote positieve of negatieve waarden van "x" 17 / (8x + 4) neigt naar nul, en de grafiek nadert de rechte lijn gegeven door de functie ja = (1/2)x - (7/4). Teken deze functie met behulp van de stippellijn.
   • Als de graad van de teller kleiner is dan de graad van de noemer, dan kun je de teller niet delen door de noemer en wordt de asymptoot beschreven door de functie Bij = 0.
   • Als de graad van de teller gelijk is aan de graad van de noemer, dan is de asymptoot een horizontale lijn gelijk aan de verhouding van de coëfficiënten bij "x" in de hoogste graad.
   • Als de graad van de teller 1 meer is dan de graad van de noemer, dan is de asymptoot een hellende rechte lijn waarvan de helling gelijk is aan de verhouding van de coëfficiënten bij "x" tot de hoogste graad.
   • Als de graad van de teller groter is dan de graad van de noemer met 2, 3, enz., dan voor grote waarden |NS| betekenis Bij neigen naar oneindig (positief of negatief) in de vorm van een vierkant, kubieke of andere graad van een polynoom. In dit geval hoeft u hoogstwaarschijnlijk geen exacte grafiek te maken van de functie die wordt verkregen door de teller te delen door de noemer.
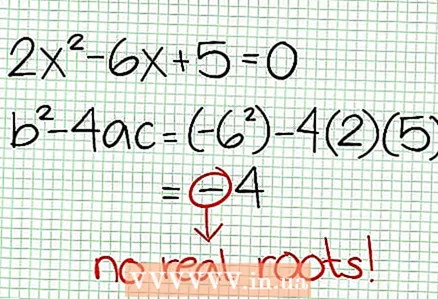3. 3 Zoek de nullen van de functie. Een rationale functie heeft nullen als de teller nul is, dat wil zeggen N (NS) = 0. In ons voorbeeld, 2x - 6x + 5 = 0. De discriminant van deze kwadratische vergelijking: B - 4ac = 6 - 4 * 2 * 5 = 36 - 40 = -4. Aangezien de discriminant negatief is, dan is N (NS), en dus F (NS) heeft geen echte wortels. De grafiek van een rationale functie snijdt de X-as niet. Als de functie nullen (wortels) heeft, plaats deze dan op het coördinatenvlak.
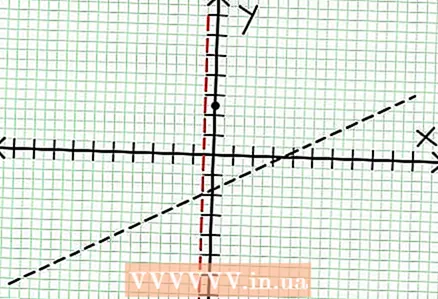4. 4 Zoek de verticale asymptoten. Om dit te doen, stelt u de noemer in op nul. In ons voorbeeld, 4x + 2 = 0 en NS = -1/2. Teken de verticale asymptoot met behulp van de stippellijn. Als voor enige waarde NS N (NS) = 0 en D (NS) = 0, dan bestaat de verticale asymptoot wel of niet (dit is een zeldzaam geval, maar het is beter om het te onthouden).
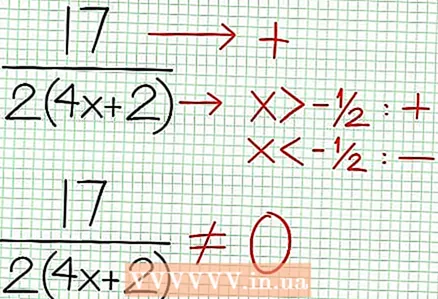5. 5 Kijk naar de rest van de teller gedeeld door de noemer. Is het positief, negatief of nul? In ons voorbeeld is de rest 17, wat positief is. Noemer 4x + 2 positief rechts van de verticale asymptoot en negatief links ervan. Dit betekent dat de grafiek van de rationale functie voor grote positieve waarden NS benadert de asymptoot van bovenaf, en voor grote negatieve waarden NS - van onder. Sinds 17 / (8x + 4) nooit gelijk is aan nul, dan zal de grafiek van deze functie nooit de door de functie gespecificeerde rechte lijn snijden Bij = (1/2)NS - (7/4).
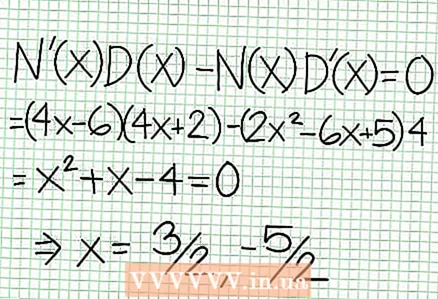6. 6 Vind lokale extremen. Er bestaat een lokaal extremum voor N '(x) NS (x) - N (x) NS '(x) = 0. In ons voorbeeld, N '(x) = 4x - 6 en D'(x) = 4. N ’(x) NS (x) - N (x) NS '(x) = (4x - 6)(4x + 2) - (2x - 6x + 5)*4 = x + x - 4 = 0. Als je deze vergelijking oplost, vind je dat x = 3/2 en x = -5/2. (Dit zijn niet helemaal nauwkeurige waarden, maar ze zijn geschikt voor ons geval wanneer superprecisie niet nodig is.)
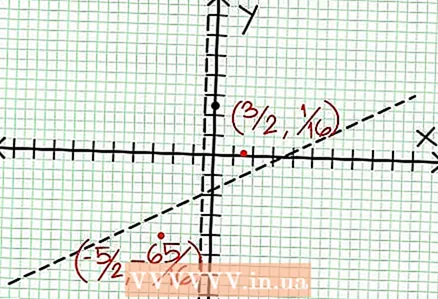7. 7 Vind de waarde Bij voor elk lokaal extremum. Vervang hiervoor de waarden NS in de oorspronkelijke rationale functie. In ons voorbeeld is f (3/2) = 1/16 en f (-5/2) = -65/16. Leg punten (3/2, 1/16) en (-5/2, -65/16) op het coördinatenvlak opzij. Aangezien de berekeningen zijn gebaseerd op geschatte waarden (uit de vorige stap), zijn het gevonden minimum en maximum ook niet helemaal nauwkeurig (maar waarschijnlijk heel dicht bij de exacte waarden). (Het punt (3/2, 1/16) ligt heel dicht bij het lokale minimum. Vanaf stap 3 weten we dat Bij altijd positief voor NS> -1/2, en we vonden een kleine waarde (1/16); dus de foutwaarde is in dit geval extreem klein.)
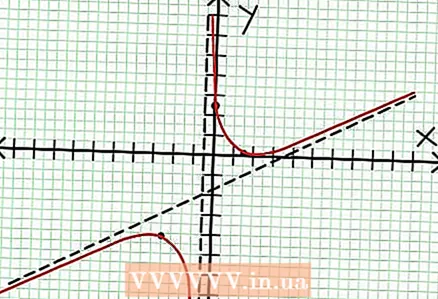8. 8 Verbind de hangende punten en breid de grafiek soepel uit naar de asymptoten (vergeet niet de juiste richting van de grafiek die de asymptoten nadert). Onthoud dat de grafiek de X-as niet mag kruisen (zie stap 3). De grafiek snijdt ook niet met de horizontale en verticale asymptoten (zie stap 5). Verander de richting van de kaart niet, behalve op de uiterste punten die in de vorige stap zijn gevonden.

Tips

• Als u de bovenstaande stappen strikt in de juiste volgorde hebt gevolgd, is het niet nodig om de tweede afgeleiden (of vergelijkbare complexe grootheden) te berekenen om uw oplossing te testen.
• Als u de waarden van hoeveelheden niet hoeft te berekenen, kunt u het vinden van lokale extremen vervangen door enkele extra coördinatenparen te berekenen (NS, Bij) tussen elk paar asymptoten. Bovendien, als het je niet uitmaakt hoe de beschreven methode werkt, wees dan niet verbaasd waarom je de afgeleide niet kunt vinden en de vergelijking N '(x) NS (x) - N (x) NS '(x) = 0.
• In sommige gevallen moet u werken met polynomen van hogere orde. Als je de exacte oplossing niet kunt vinden met factorisatie, formules, enz., schat dan mogelijke oplossingen met behulp van numerieke methoden zoals de methode van Newton.
• In zeldzame gevallen delen de teller en noemer een gemeenschappelijke variabele factor. Volgens de beschreven stappen zal dit leiden tot nul en een verticale asymptoot op dezelfde plaats. Dit is echter niet mogelijk en de verklaring is een van de volgende:
  • Nul in N (NS) heeft een hogere multipliciteit dan nul in D (NS). Grafiek F (NS) neigt op dit punt naar nul, maar wordt daar niet gedefinieerd. Geef dit aan door een cirkel om het punt te tekenen.
  • Nul in N (NS) en nul in D (NS) hebben dezelfde veelvoud. De grafiek nadert een niet-nulpunt bij deze waarde NSmaar daarin niet gedefinieerd. Geef dit aan door een cirkel om het punt te tekenen.
  • Nul in N (NS) heeft een lagere multipliciteit dan nul in D (NS). Er is hier een verticale asymptoot.