Inhoud

• Stappen
• Advies

Als u een wiskundige of een grafisch programmeur bent, moet u mogelijk de hoek tussen twee gegeven vectoren vinden. In dit artikel laat wikiHow zien hoe je dat moet doen.

Stappen

Deel 1 van 2: Zoek de hoek tussen twee vectoren

1. 

   Vector definitie. Schrijf alle informatie op over de twee vectoren die je hebt. Stel dat u alleen de gespecificeerde parameters van hun dimensionale coördinaten (ook wel componenten genoemd) heeft. Als u de lengte (magnitude) van een vector al kent, kunt u enkele van de onderstaande stappen overslaan.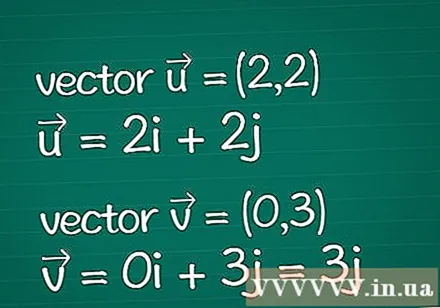
   • Voorbeeld: tweedimensionale vector = (2,2) en tweedimensionale vector = (0,3). Ze kunnen ook worden geschreven als = 2ik + 2j en = 0ik + 3j = 3j.
   • Hoewel in het voorbeeld in dit artikel tweedimensionale vectoren worden gebruikt, kunnen de volgende instructies van toepassing zijn op vectoren met een willekeurig aantal dimensies.

2. 

   
   
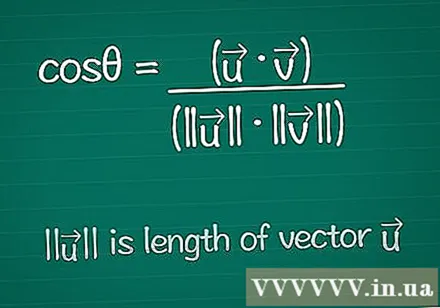
   Schrijf de cosinusformule op. Om de hoek θ tussen twee vectoren te vinden, beginnen we met de formule voor het vinden van de cosinus voor die hoek. U kunt hieronder meer te weten komen over deze formule of het gewoon als volgt opschrijven:
   • cosθ = (•) / (|||| ||||)
   • |||| betekent "lengte van de vector".
   • • is het scalaire product van de twee vectoren - dit wordt hieronder uitgelegd.

3. 

   
   
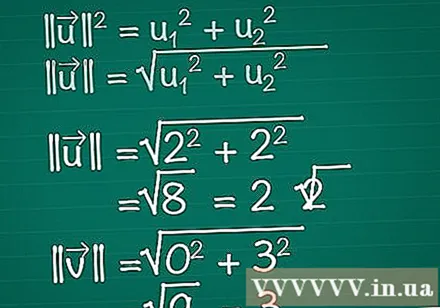
   Bereken de lengte van elke vector. Stel je een rechthoekige driehoek voor die bestaat uit de x-, y-componenten van de vector en de vector zelf. De vector vormt de hypotenusa van de driehoek, dus om de lengte te bepalen gebruiken we de stelling van Pythagoras. In feite kan deze formule gemakkelijk worden uitgebreid tot een vector met een willekeurig aantal dimensies.
   • || u || = u₁ + u₂. Als een vector meer dan twee elementen heeft, hoeft u alleen maar + u toe te voegen₃ + u₄ +...
   • Vandaar dat voor een tweedimensionale vector, || u || = √ (u₁ + u₂).
   • In dit voorbeeld |||| = √ (2 + 2) = √ (8) = 2√2. |||| = √(0 + 3) = √(9) = 3.

4. 

   
   
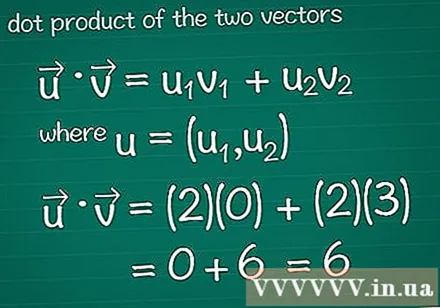
   Bereken het scalaire product van twee vectoren. Misschien heb je de methode van vectorvermenigvuldiging geleerd, ook wel bekend als scalair deze. Om het scalaire product ten opzichte van hun samenstelling te berekenen, vermenigvuldigt u de ingrediënten in elke richting samen en telt u vervolgens het volledige resultaat op.
   • Raadpleeg voor het grafische programma Tips voordat u verder leest.
   • In wiskunde • = u₁v₁ + u₂v₂, waar, u = (u₁, u₂). Als de vector meer dan twee elementen heeft, voegt u gewoon + u toe₃v₃ + u₄v₄...
   • In dit voorbeeld • = u₁v₁ + u₂v₂ = (2)(0) + (2)(3) = 0 + 6 = 6. Dit is het scalaire product van de vector en de vector.

5. 

   Zet de resultaten in de formule. Onthoud dat cosθ = (•) / (|||| || ||). Nu kennen we zowel het scalaire product als de lengte van elke vector. Voer deze in de formule in om de cosinus van de hoek te berekenen.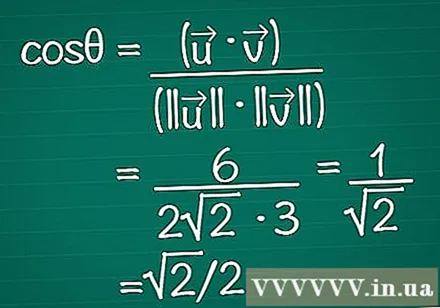
   • In ons voorbeeld cosθ = 6 / (2√2 * 3) = 1 / √2 = √2 / 2.

6. 

   Zoek de hoek op basis van de cosinus. U kunt de functie arccos of cos in een rekenmachine gebruiken om θ uit een bekende cos-waarde te vinden. Bij sommige resultaten kunt u de hoek vinden op basis van de eenheidscirkel.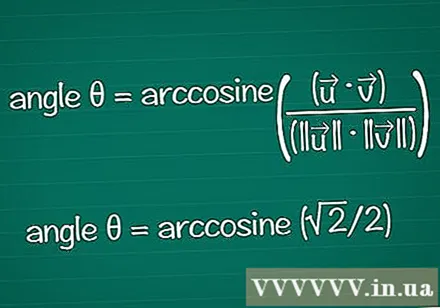
   • In het voorbeeld cosθ = √2 / 2. Typ "arccos (√2 ​​/ 2)" in je rekenmachine om de hoek te vinden. Of je kunt hoek θ op de eenheidscirkel vinden, op positie cosθ = √2 / 2. Het is waar voor θ = /₄ of 45º.
   • Alles combineren, de uiteindelijke formule is: hoek θ = arccosine ((•) / (|||| || ||))
   advertentie

Deel 2 van 2: Bepaling van de hoekformule

1. 

   Begrijp het doel van de formule. Deze formule is niet afgeleid van bestaande regels. In plaats daarvan wordt het gevormd als de definitie van het scalaire product en de hoek tussen de twee vectoren. Toch was het geen willekeurige beslissing. Terugkomend op de basisgeometrie, kunnen we begrijpen waarom deze formule intuïtieve en bruikbare definities biedt.
   • De onderstaande voorbeelden gebruiken tweedimensionale vectoren omdat ze het gemakkelijkst te begrijpen en het eenvoudigst zijn. Driedimensionale of meer vectoren hebben eigenschappen die worden gedefinieerd door bijna vergelijkbare algemene formules.

2. 

   Bekijk de stelling van Cosine. Beschouw een gewone driehoek met hoek θ tussen zijden a en b, tegenoverliggende zijde c. De cosinusstelling stelt dat c = a + b -2abcos(θ). Dit resultaat is heel eenvoudig ontleend aan de basisgeometrie.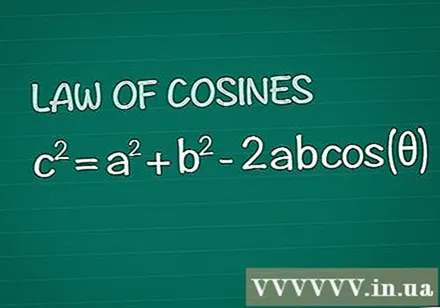

3. 

   Verbind twee vectoren en vorm een ​​driehoek. Teken een paar tweedimensionale vectoren op papier, vectoren en vectoren, waarbij θ de hoek ertussen is. Teken een derde vector tussen deze twee om een ​​driehoek te maken. Met andere woorden, teken een vector zodanig dat + =. Vector = -.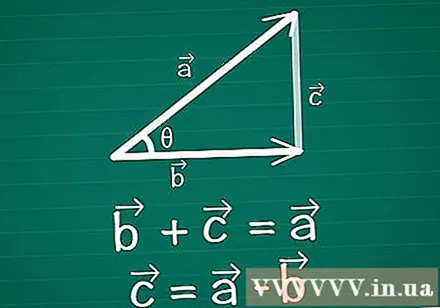

4. 

   Schrijf de cosinusstelling voor deze driehoek. Vervang de zijdelengte van onze "vectordriehoek" in de cosinusstelling:
   • || (a - b) || = || een || + || b || - 2 || een || || b ||cos(θ)

5. 

   Herschrijf met scalair product. Onthoud dat een scalair product de afbeelding is van de ene vector op de andere. Het scalaire product van een vector met zichzelf vereist geen projectie, want hier is er geen verschil in richting. Dat betekent • = || a ||. Hiermee herschrijven we de vergelijking:
   • (-) • (-) = • + • - 2 || a || || b ||cos(θ)

6. 

   Herschreef dezelfde formule met succes. Vouw de linkerkant van de formule uit en vereenvoudig de formule om de formule te gebruiken om hoeken te vinden.
   • • - • - • + • = • + • - 2 || a || || b ||cos(θ)
   • - • - • = -2 || a || || b ||cos(θ)
   • -2 (•) = -2 || a || || b ||cos(θ)
   • • = || een || || b ||cos(θ)
   advertentie

Advies

• Om waarden te wijzigen en het probleem snel op te lossen, gebruikt u deze formule voor elk paar tweedimensionale vectoren: cosθ = (u₁ • v₁ + u₂ • v₂) / (√ (u₁ • u₂) • √ (v₁ • v₂)).
• Als u met grafische software voor computers werkt, is de kans groot dat u zich alleen zorgen hoeft te maken over de dimensie van vectoren zonder u zorgen te maken over hun lengte. Gebruik de volgende stappen om een ​​vergelijking in te korten en uw programma te versnellen:
  • Normaliseer elke vector zodat ze gelijk zijn aan 1. Om dit te doen, deelt u elk van de vectorcomponenten door zijn lengte.
  • Verkrijg het genormaliseerde product van de scalair in plaats van de originele vector.
  • Omdat de lengte 1 is, kunnen we de lengte-elementen uitsluiten van de vergelijking. Ten slotte is de verkregen hoekvergelijking arccos (•).
• Op basis van de cosinusformule kunnen we snel bepalen of de hoek acuut of stomp is. Begin met cosθ = (•) / (|||| ||||):
  • De linker- en rechterkant van de vergelijking moeten hetzelfde teken hebben (positief of negatief).
  • Omdat lengte altijd positief is, moet cosθ hetzelfde teken hebben als het scalaire product.
  • Dus als het product positief is, is cosθ ook positief. We bevinden ons in het eerste kwadrant van de eenheidscirkel, met θ <π / 2 of 90º. De te vinden hoek is de scherpe hoek.
  • Als het scalaire product negatief is, is cosθ negatief. We bevinden ons in het tweede kwadrant van de eenheidscirkel, met π / 2 <θ ≤ π of 90º <θ ≤ 180º. Dat is de gevangenishoek.