Inhoud

• Stappen

Een goniometrische vergelijking bevat een of meer goniometrische functies van de variabele "x" (of een andere variabele). Het oplossen van een trigonometrische vergelijking is het vinden van zo'n waarde "x" die voldoet aan de functie(s) en de vergelijking als geheel.

• Oplossingen voor goniometrische vergelijkingen worden uitgedrukt in graden of radialen. Voorbeelden:

x = / 3; x = 5π / 6; x = 3π / 2; x = 45 graden; x = 37,12 graden; x = 178,37 graden.

• Let op: de waarden van goniometrische functies uit hoeken, uitgedrukt in radialen, en uit hoeken, uitgedrukt in graden, zijn gelijk. Een goniometrische cirkel met een straal gelijk aan één wordt gebruikt om goniometrische functies te beschrijven, en om de juistheid van de oplossing van de trigonometrische basisvergelijkingen en ongelijkheden te controleren.
• Voorbeelden van goniometrische vergelijkingen:
  • zonde x + zonde 2x = 1/2; tg x + ctg x = 1,732;
  • cos 3x + sin 2x = cos x; 2sin 2x + cos x = 1.

1. Een trigonometrische cirkel met een straal van één (eenheidscirkel).
   • Het is een cirkel met een straal gelijk aan één en middelpunt op punt O. De eenheidscirkel beschrijft 4 trigonometrische basisfuncties van de variabele "x", waarbij "x" de hoek is gemeten vanuit de positieve richting van de X-as tegen de klok in.
   • Als "x" een hoek is op de eenheidscirkel, dan:
   • De horizontale as OAx definieert de functie F (x) = cos x.
   • De verticale as OBy definieert de functie F (x) = sin x.
   • De verticale as AT definieert de functie F (x) = tan x.
   • De horizontale as BU definieert de functie F (x) = ctg x.

• De eenheidscirkel wordt ook gebruikt om trigonometrische basisvergelijkingen en ongelijkheden op te lossen (er worden verschillende posities van "x" op beschouwd).

Stappen

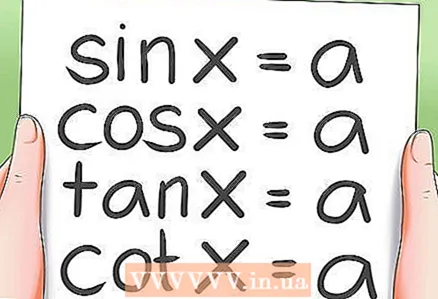1. 1 Het concept van het oplossen van trigonometrische vergelijkingen.
   • Om een ​​goniometrische vergelijking op te lossen, converteert u deze naar een of meer trigonometrische basisvergelijkingen. Het oplossen van een trigonometrische vergelijking komt uiteindelijk neer op het oplossen van vier basis trigonometrische vergelijkingen.
2. 2 Het oplossen van trigonometrische basisvergelijkingen.
   • Er zijn 4 soorten trigonometrische basisvergelijkingen:
   • zonde x = een; cos x = a
   • tgx = een; ctg x = a
   • Het oplossen van trigonometrische basisvergelijkingen omvat het kijken naar de verschillende x-posities op de eenheidscirkel en het gebruik van een conversietabel (of rekenmachine).
   • Voorbeeld 1.sin x = 0,866. Met behulp van een conversietabel (of rekenmachine) krijg je het antwoord: x = π / 3. De eenheidscirkel geeft een ander antwoord: 2π / 3. Onthoud: alle trigonometrische functies zijn periodiek, dat wil zeggen dat hun waarden worden herhaald. Bijvoorbeeld, de periodiciteit van sin x en cos x is 2πn, en de periodiciteit van tg x en ctg x is πn. Daarom is het antwoord als volgt geschreven:
   • x1 = π / 3 + 2πn; x2 = 2π / 3 + 2πn.
   • Voorbeeld 2.cos x = -1/2. Met behulp van een conversietabel (of rekenmachine) krijg je het antwoord: x = 2π / 3. De eenheidscirkel geeft een ander antwoord: -2π / 3.
   • x1 = 2π / 3 + 2π; x2 = -2π / 3 + 2π.
   • Voorbeeld 3.tg (x - π / 4) = 0.
   • Antwoord: x = π / 4 + πn.
   • Voorbeeld 4. ctg 2x = 1.732.
   • Antwoord: x = π / 12 + πn.
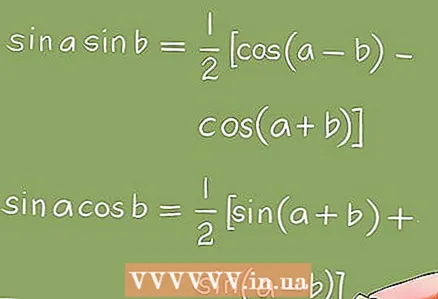3. 3 Transformaties die worden gebruikt om trigonometrische vergelijkingen op te lossen.
   • Om trigonometrische vergelijkingen te transformeren, worden algebraïsche transformaties (factorisatie, reductie van homogene termen, enz.) en trigonometrische identiteiten gebruikt.
   • Voorbeeld 5. Met behulp van trigonometrische identiteiten wordt de vergelijking sin x + sin 2x + sin 3x = 0 omgezet in de vergelijking 4cos x * sin (3x / 2) * cos (x / 2) = 0. U moet dus los de volgende trigonometrische basisvergelijkingen op: cos x = 0; zonde (3x / 2) = 0; cos (x / 2) = 0.
     
     
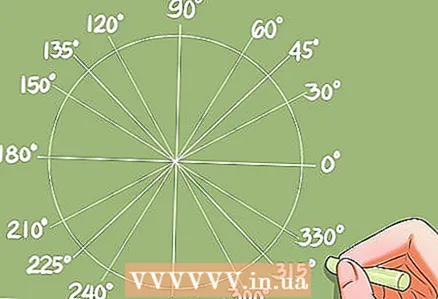
4. 4 Hoeken vinden uit bekende waarden van functies.
   • Voordat u methoden leert voor het oplossen van trigonometrische vergelijkingen, moet u leren hoe u hoeken kunt vinden uit bekende waarden van functies. Dit kan met behulp van een conversietabel of rekenmachine.
   • Voorbeeld: cos x = 0,732. De rekenmachine geeft het antwoord x = 42,95 graden. De eenheidscirkel geeft extra hoeken, waarvan de cosinus ook 0,732 is.
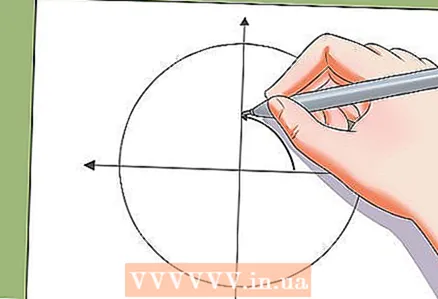5. 5 Zet de oplossing opzij op de eenheidscirkel.
   • U kunt de oplossingen van de trigonometrische vergelijking op de eenheidscirkel uitstellen. De oplossingen van de trigonometrische vergelijking op de eenheidscirkel zijn de hoekpunten van een regelmatige veelhoek.
   • Voorbeeld: De oplossingen x = π / 3 + πn / 2 op de eenheidscirkel zijn de hoekpunten van een vierkant.
   • Voorbeeld: De oplossingen x = π / 4 + πn / 3 op de eenheidscirkel vertegenwoordigen de hoekpunten van een regelmatige zeshoek.
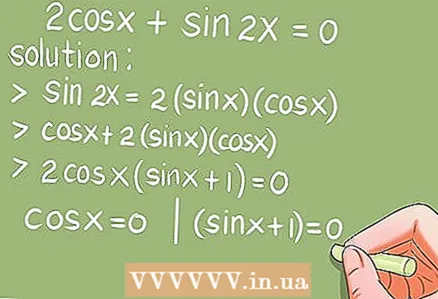6. 6 Methoden voor het oplossen van trigonometrische vergelijkingen.
   • Als een gegeven goniometrische vergelijking slechts één goniometrische functie bevat, los die vergelijking dan op als de basis goniometrische vergelijking.Als een gegeven vergelijking twee of meer trigonometrische functies bevat, zijn er 2 methoden om een ​​dergelijke vergelijking op te lossen (afhankelijk van de mogelijkheid van transformatie).
     • Methode 1.
   • Zet deze vergelijking om in een vergelijking van de vorm: f (x) * g (x) * h (x) = 0, waarbij f (x), g (x), h (x) de trigonometrische basisvergelijkingen zijn.
     
     
   • Voorbeeld 6.2cos x + sin 2x = 0. (0 x 2π)
   • Oplossing. Gebruik de dubbele hoekformule sin 2x = 2 * sin x * cos x, vervang sin 2x.
   • 2cos x + 2 * sin x * cos x = 2cos x * (sin x + 1) = 0. Los nu de twee trigonometrische basisvergelijkingen op: cos x = 0 en (sin x + 1) = 0.
   • Voorbeeld 7.cos x + cos 2x + cos 3x = 0. (0 x 2π)
   • Oplossing: Transformeer deze vergelijking met behulp van trigonometrische identiteiten in een vergelijking van de vorm: cos 2x (2cos x + 1) = 0. Los nu de twee trigonometrische basisvergelijkingen op: cos 2x = 0 en (2cos x + 1) = 0.
   • Voorbeeld 8.sin x - sin 3x = cos 2x. (0 x 2π)
   • Oplossing: Transformeer deze vergelijking met behulp van trigonometrische identiteiten in een vergelijking van de vorm: -cos 2x * (2sin x + 1) = 0. Los nu de twee trigonometrische basisvergelijkingen op: cos 2x = 0 en (2sin x + 1) = 0.
     • Methode 2.
   • Zet de gegeven goniometrische vergelijking om in een vergelijking die slechts één goniometrische functie bevat. Vervang deze goniometrische functie dan door een onbekende, bijvoorbeeld t (sin x = t; cos x = t; cos 2x = t, tg x = t; tg (x / 2) = t, etc.).
   • Voorbeeld 9.3sin ^ 2 x - 2cos ^ 2 x = 4sin x + 7 (0 x 2π).
   • Oplossing. Vervang in deze vergelijking (cos ^ 2 x) door (1 - sin ^ 2 x) (door identiteit). De getransformeerde vergelijking is:
   • 3sin ^ 2 x - 2 + 2sin ^ 2 x - 4sin x - 7 = 0. Vervang sin x door t. De vergelijking ziet er nu als volgt uit: 5t ^ 2 - 4t - 9 = 0. Dit is een kwadratische vergelijking met twee wortels: t1 = -1 en t2 = 9/5. De tweede wortel t2 voldoet niet aan het waardenbereik van de functie (-1 sin x 1). Beslis nu: t = sin x = -1; x = 3π / 2.
   • Voorbeeld 10.tg x + 2 tg ^ 2 x = ctg x + 2
   • Oplossing. Vervang tg x door t. Herschrijf de oorspronkelijke vergelijking als volgt: (2t + 1) (t ^ 2 - 1) = 0. Zoek nu t en zoek dan x voor t = tg x.
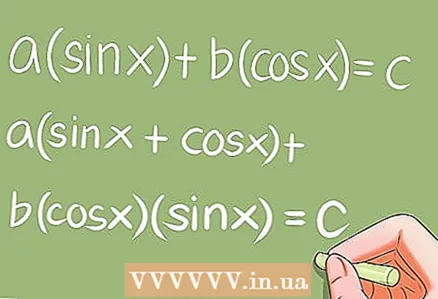7. 7 Speciale trigonometrische vergelijkingen.
   • Er zijn verschillende speciale trigonometrische vergelijkingen die specifieke transformaties vereisen. Voorbeelden:
   • a * sin x + b * cos x = c; a (sin x + cos x) + b * cos x * sin x = c;
   • a * sin ^ 2 x + b * sin x * cos x + c * cos ^ 2 x = 0
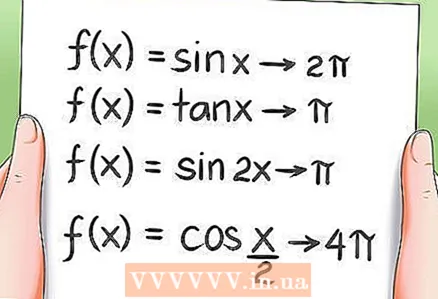8. 8 Periodiciteit van goniometrische functies.
   • Zoals eerder vermeld, zijn alle trigonometrische functies periodiek, dat wil zeggen dat hun waarden na een bepaalde periode worden herhaald. Voorbeelden:
     • De periode van de functie f (x) = sin x is 2π.
     • De periode van de functie f (x) = tan x is gelijk aan π.
     • De periode van de functie f (x) = sin 2x is π.
     • De periode van de functie f (x) = cos (x / 2) is 4π.
   • Als de periode in de opgave is gespecificeerd, bereken dan de waarde "x" binnen deze periode.
   • Opmerking: het oplossen van goniometrische vergelijkingen is geen gemakkelijke taak en leidt vaak tot fouten. Controleer je antwoorden dus goed. Om dit te doen, kunt u een grafische rekenmachine gebruiken om de gegeven vergelijking R (x) = 0 te plotten. In dergelijke gevallen worden oplossingen weergegeven als decimale breuken (dat wil zeggen, π wordt vervangen door 3,14).