Inhoud

• Stappen
• Advies

In tegenstelling tot een rechte lijn, verandert de hoekcoëfficiënt (helling) continu terwijl deze langs de curve beweegt. Calculus geeft het idee dat elk punt op de grafiek kan worden uitgedrukt als een hoekcoëfficiënt of "instantane veranderingssnelheid". De raaklijn op een punt is een lijn met dezelfde hoekcoëfficiënt en loopt door hetzelfde punt. Om een ​​raaklijnvergelijking te vinden, moet u weten hoe u de oorspronkelijke vergelijking kunt afleiden.

Stappen

Methode 1 van 2: Zoek de vergelijking voor de raaklijn

1. 

   Grafiekfuncties en raaklijnen (deze stap is optioneel, maar aanbevolen). De tabel zal u helpen het probleem gemakkelijker te begrijpen en te controleren of het antwoord redelijk is of niet. Teken functiegrafieken op rasterpapier, gebruik indien nodig de wetenschappelijke rekenmachine met grafiekfunctie als referentie. Trek een raaklijn door een bepaald punt (onthoud dat de raaklijn door dat punt gaat en dezelfde helling heeft als de grafiek daar).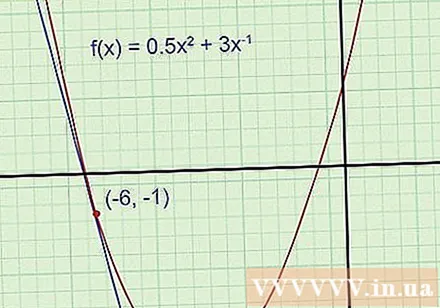
   • Voorbeeld 1: Parabolische tekening. Trek een raaklijn door het punt (-6, -1).
     Ook al ken je de raaklijnvergelijking niet, je kunt nog steeds zien dat de helling negatief is en het snijpunt negatief (ver onder het parabolische hoekpunt met de ordinaat van -5,5). Als het uiteindelijke antwoord dat u vindt niet overeenkomt met deze details, moet er een fout in uw berekening zitten en moet u het opnieuw controleren.

2. 

   
   
   Verkrijg de eerste afgeleide om de vergelijking te vinden helling van de raaklijn. Met de functie f (x) vertegenwoordigt de eerste afgeleide f '(x) de vergelijking voor de helling van de raaklijn op elk punt op f (x). Er zijn veel manieren om derivaten te gebruiken. Hier is een eenvoudig voorbeeld met behulp van de machtsregel:
   • Voorbeeld 1 (vervolg): De grafiek wordt gegeven door een functie.
     Herinnerend aan de machtsregel bij het nemen van een afgeleide:.
     De eerste afgeleide van de functie = f '(x) = (2) (0.5) x + 3-0.
     f '(x) = x + 3. Vervang x door een willekeurige waarde a, de vergelijking geeft ons de helling van de raaklijnfunctie f (x) op punt x = a.

3. 

   
   
   Voer de x-waarde van het punt in kwestie in. Lees de opgave om de coördinaten van het punt te vinden om de raaklijn te vinden. Voer de coördinaat van dit punt in f '(x) in. Het verkregen resultaat is de helling van de raaklijn op het bovenstaande punt.
   • Voorbeeld 1 (vervolg): Het punt dat in het artikel wordt genoemd, is (-6, -1). Diagonale -6 spanning gebruiken in f '(x):
     f '(- 6) = -6 + 3 = -3
     De helling van de raaklijn is -3.

4. 

   
   
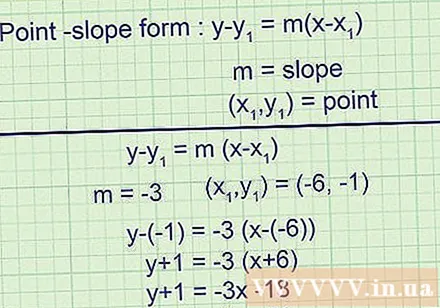
   Schrijf een raaklijnvergelijking in de vorm van een rechte lijn en ken de coëfficiënt van de hoek en een punt erop. Deze lineaire vergelijking wordt geschreven als. Binnen, m is de helling en is een punt op de raaklijn. Je hebt nu alle informatie die je nodig hebt om in dit formulier een raakvergelijking te schrijven.
   • Voorbeeld 1 (vervolg):
     De helling van de raaklijn is -3, dus:
     De raaklijn loopt door het punt (-6, -1), dus de laatste vergelijking is:
     Kortom, we kunnen:
     

5. 

   Grafische bevestiging. Als je een grafische rekenmachine hebt, zet dan de originele functie en de raaklijn uit om te controleren of het antwoord juist is. Als u berekeningen op papier doet, gebruik dan eerder getekende grafieken om er zeker van te zijn dat uw antwoord geen duidelijke fouten bevat.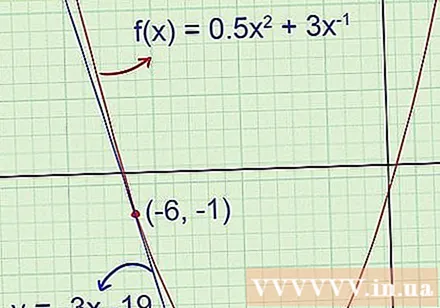
   • Voorbeeld 1 (vervolg): De eerste tekening laat zien dat de raaklijn negatieve hoekcoëfficiënten heeft en dat de offset ver onder -5,5 ligt. De zojuist gevonden tangensvergelijking is y = -3x -19, wat betekent dat -3 de helling van de hoek is en -19 de ordinaat.

6. 

   Probeer een moeilijker probleem op te lossen. We doorlopen alle bovenstaande stappen nogmaals.Op dit punt is het doel om de tangens van op x = 2 te vinden: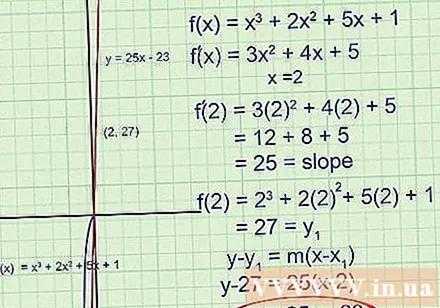
   • Zoek de eerste afgeleide met behulp van de machtsregel :. Deze functie geeft ons de helling van de raaklijn.
   • Zoek voor x = 2. Dit is de helling bij x = 2.
   • Merk op dat we deze keer geen punt hebben en alleen de x-coördinaat. Om de y-coördinaat te vinden, vervangt u x = 2 in de oorspronkelijke functie :. De score is (2,27).
   • Schrijf een vergelijking voor een raaklijn die door een punt gaat en laat de coëfficiënt van de hoek bepalen:
     
     Vereenvoudig indien nodig tot y = 25x - 23.
   advertentie

Methode 2 van 2: Los gerelateerde problemen op

1. 

   Zoek het uiterste in de grafiek. Het zijn de punten waarop de grafiek een lokaal maximum nadert (een punt hoger dan aangrenzende punten aan beide kanten) of een lokaal minimum (lager dan aangrenzende punten aan beide kanten). De raaklijn heeft op deze punten altijd een nulcoëfficiënt (een horizontale lijn). De coëfficiënt van de hoek is echter niet voldoende om te concluderen dat dit het uiterste punt is. Hier leest u hoe u ze kunt vinden: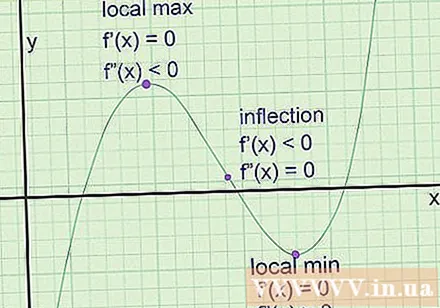
   • Neem de eerste afgeleide van de functie om f '(x) te krijgen, de helling van de helling van de raaklijn.
   • Los de vergelijking f '(x) = 0 op om het uiterste punt te vinden potentieel.
   • Als we de kwadratische afgeleide nemen om f '(x) te krijgen, vertelt de vergelijking ons de snelheid waarmee de helling van de raaklijn verandert.
   • Verander bij elk potentieel uiterste de coördinaat een in f '' (x). Als f '(a) positief is, hebben we een lokaal minimum op een. Als f '(a) negatief is, hebben we een lokaal maximum punt. Als f '(a) 0 is, zal het niet het uiterste zijn, het is een buigpunt.
   • Als max of min bereikt op een, zoek f (a) om het snijpunt te bepalen.

2. 

   Zoek de vergelijkingen van de normaal. De "normale" lijn van een kromme op een bepaald punt a loopt door dat punt en staat loodrecht op de raaklijn. Om de vergelijking voor de normaal te vinden, gebruik je het volgende: (helling van de normaal) (helling van de normaal) = -1 wanneer ze hetzelfde punt op de grafiek passeren. Specifiek: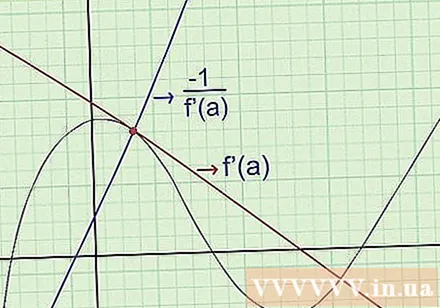
   • Zoek f '(x), de helling van de raaklijn.
   • Als we op een bepaald punt x = hebben een: zoek f '(a) om de helling op dat punt te bepalen.
   • Bereken om de coëfficiënt van de normaal te vinden.
   • Schrijf de vergelijking voor de loodlijn om de coëfficiënten van de hoek en een punt waar het doorheen gaat te kennen.
   advertentie

Advies

• Herschrijf indien nodig de originele vergelijking in standaardvorm: f (x) = ... of y = ...