Inhoud

• Stappen
• Methode 1 van 3: Hoe een derdegraadsvergelijking op te lossen zonder een constante term
• Methode 2 van 3: Hoe hele wortels te vinden met behulp van multipliers
• Methode 3 van 3: Hoe een vergelijking op te lossen met behulp van de discriminant?

In een derdegraadsvergelijking is de hoogste exponent 3, zo'n vergelijking heeft 3 wortels (oplossingen) en heeft de vorm ${ displaystyle bijl ^ {3} + bx ^ {2} + cx + d = 0}$... Sommige derdegraadsvergelijkingen zijn niet zo eenvoudig op te lossen, maar als je de juiste methode toepast (met een goede theoretische achtergrond), kun je de wortels van zelfs de meest complexe derdegraadsvergelijking vinden - gebruik hiervoor de formule voor het oplossen van de kwadratische vergelijking, vind de hele wortels, of bereken de discriminant.

Stappen

Methode 1 van 3: Hoe een derdegraadsvergelijking op te lossen zonder een constante term

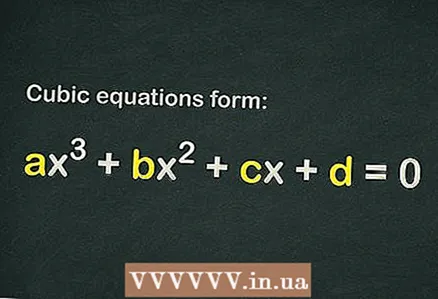1. 1 Zoek uit of er een vrije term in de derdegraadsvergelijking is NS{ weergavestijl d}. De derdegraadsvergelijking heeft de vorm ${ displaystyle bijl ^ {3} + bx ^ {2} + cx + d = 0}$... Om een ​​vergelijking als kubisch te beschouwen, is het voldoende dat alleen de term ${ weergavestijl x ^ {3}}$ (dat wil zeggen, er mogen helemaal geen andere leden zijn).
   • Als de vergelijking een vrije term heeft ${ weergavestijl d}$, gebruik een andere methode.
   • Als in de vergelijking ${ weergavestijl a = 0}$, het is niet kubisch.
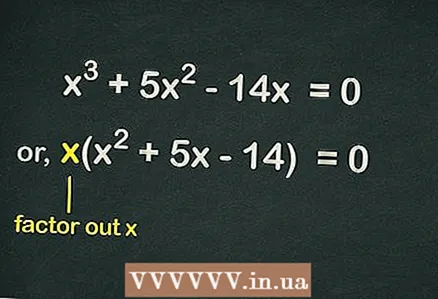2. 2 Haal uit de haakjes x{ weergavestijl x}. Omdat er geen vrije term in de vergelijking is, bevat elke term in de vergelijking de variabele ${ weergavestijl x}$... Dit betekent dat een ${ weergavestijl x}$ kan worden uitgesloten van haakjes om de vergelijking te vereenvoudigen. De vergelijking wordt dus als volgt geschreven: ${ displaystyle x (ax ^ {2} + bx + c)}$.
   • Bijvoorbeeld, gegeven een derdegraadsvergelijking ${ weergavestijl 3x ^ {3} -2x ^ {2} + 14x = 0}$
   • Afhaalmaaltijd ${ weergavestijl x}$ haakjes en krijg ${ weergavestijl x (3x ^ {2} -2x + 14) = 0}$
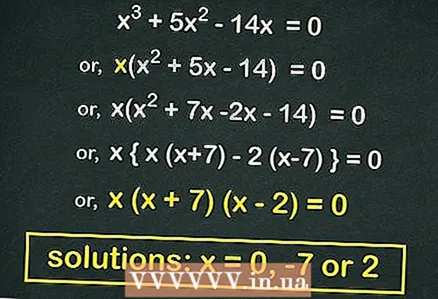3. 3 Factor (het product van twee binomials) de kwadratische vergelijking (indien mogelijk). Veel kwadratische vergelijkingen van de vorm ${ displaystyle bijl ^ {2} + bx + c = 0}$ factoriseren kan. Zo'n vergelijking zal blijken als we nemen ${ weergavestijl x}$ buiten de haakjes. In ons voorbeeld:
   • Haal uit de haakjes ${ weergavestijl x}$: ${ weergavestijl x (x ^ {2} + 5x-14) = 0}$
   • Factor de kwadratische vergelijking: ${ weergavestijl x (x + 7) (x-2) = 0}$
   • Stel elke bak gelijk aan ${ weergavestijl 0}$... De wortels van deze vergelijking zijn ${ weergavestijl x = 0, x = -7, x = 2}$.
4. 4 Los een kwadratische vergelijking op met een speciale formule. Doe dit als de kwadratische vergelijking niet kan worden ontbonden. Om twee wortels van een vergelijking te vinden, de waarden van de coëfficiënten ${ weergavestijl a}$, ${ weergavestijl b}$, ${ weergavestijl c}$ vervang in de formule ${ displaystyle { frac {-b pm { sqrt {b ^ {2} -4ac}}} {2a}}}$.
   • Vervang in ons voorbeeld de waarden van de coëfficiënten ${ weergavestijl a}$, ${ weergavestijl b}$, ${ weergavestijl c}$ (${ weergavestijl 3}$, ${ weergavestijl -2}$, ${ weergavestijl 14}$) in de formule:

     ${ displaystyle { frac {-b pm { sqrt {b ^ {2} -4ac}}} {2a}}}$

     ${ displaystyle { frac {- (- 2) pm { sqrt {((-2) ^ {2} -4 (3) (14)}}} {2 (3)}}}$

     ${ displaystyle { frac {2 pm { sqrt {4- (12) (14)}}} {6}}}$

     ${ displaystyle { frac {2 pm { sqrt {(4-168}}} {6}}}$

     ${ displaystyle { frac {2 pm { sqrt {-164}}} {6}}}$

   • Eerste wortel:

     ${ displaystyle { frac {2 + { sqrt {-164}}} {6}}}$

     ${ weergavestijl { frac {2 + 12,8i} {6}}}$

   • Tweede wortel:

     ${ weergavestijl { frac {2-12,8i} {6}}}$

5. 5 Gebruik nul- en kwadratische wortels als oplossingen voor de derdegraadsvergelijking. Kwadratische vergelijkingen hebben twee wortels, terwijl kubieke vergelijkingen er drie hebben. Je hebt al twee oplossingen gevonden - dit zijn de wortels van de kwadratische vergelijking. Als u "x" buiten de haakjes plaatst, zou de derde oplossing zijn: ${ weergavestijl 0}$.
   • Als je "x" uit de haakjes haalt, krijg je ${ displaystyle x (ax ^ {2} + bx + c) = 0}$, dat wil zeggen, twee factoren: ${ weergavestijl x}$ en een kwadratische vergelijking tussen haakjes. Als een van deze factoren is ${ weergavestijl 0}$, de hele vergelijking is ook gelijk aan ${ weergavestijl 0}$.
   • Twee wortels van een kwadratische vergelijking zijn dus oplossingen van een derdegraadsvergelijking. De derde oplossing is: ${ weergavestijl x = 0}$.

Methode 2 van 3: Hoe hele wortels te vinden met behulp van multipliers

1. 1 Zorg ervoor dat er een vrije term in de derdegraadsvergelijking staat NS{ weergavestijl d}. Als in een vergelijking van de vorm ${ displaystyle bijl ^ {3} + bx ^ {2} + cx + d = 0}$ er is een gratis lid ${ weergavestijl d}$ (wat niet gelijk is aan nul), zal het niet werken om "x" buiten de haakjes te plaatsen. Gebruik in dat geval de methode die in deze sectie wordt beschreven.
   • Bijvoorbeeld, gegeven een derdegraadsvergelijking ${ weergavestijl 2x ^ {3} + 9x ^ {2} + 13x = -6}$... Om nul aan de rechterkant van de vergelijking te krijgen, voegt u toe ${ weergavestijl 6}$ aan beide kanten van de vergelijking.
   • De vergelijking zal blijken ${ weergavestijl 2x ^ {3} + 9x ^ {2} + 13x + 6 = 0}$... Zoals ${ weergavestijl d = 6}$, kan de in de eerste sectie beschreven methode niet worden gebruikt.
2. 2 Noteer de factoren van de coëfficiënt een{ weergavestijl a} en een gratis lid NS{ weergavestijl d}. Dat wil zeggen, zoek de factoren van het getal op ${ weergavestijl x ^ {3}}$ en cijfers voor het gelijkteken. Bedenk dat de factoren van een getal de getallen zijn die, wanneer vermenigvuldigd, dat getal opleveren.
   • Om bijvoorbeeld het nummer te krijgen 6, je moet vermenigvuldigen ${ weergavestijl 6 keer 1}$ en ${ weergavestijl 2 keer 3}$... Dus de cijfers 1, 2, 3, 6 zijn factoren van het getal 6.
   • In onze vergelijking ${ weergavestijl a = 2}$ en ${ weergavestijl d = 6}$... Vermenigvuldigers 2 zijn 1 en 2... Vermenigvuldigers 6 zijn de cijfers 1, 2, 3 en 6.
3. 3 Verdeel elke factor een{ weergavestijl a} voor elke factor NS{ weergavestijl d}. Als resultaat krijg je veel breuken en meerdere gehele getallen; de wortels van de derdegraadsvergelijking zullen een van de gehele getallen zijn of de negatieve waarde van een van de gehele getallen.
   • Verdeel in ons voorbeeld de factoren ${ weergavestijl a}$ (1 en 2) door factoren ${ weergavestijl d}$ (1, 2, 3 en 6). Je krijgt: ${ weergavestijl 1}$, ${ displaystyle { frac {1} {2}}}$, ${ weergavestijl { frac {1} {3}}}$, ${ weergavestijl { frac {1} {6}}}$, ${ weergavestijl 2}$ en ${ weergavestijl { frac {2} {3}}}$... Voeg nu negatieve waarden van de verkregen breuken en getallen toe aan deze lijst: ${ weergavestijl 1}$, ${ weergavestijl -1}$, ${ displaystyle { frac {1} {2}}}$, ${ displaystyle - { frac {1} {2}}}$, ${ weergavestijl { frac {1} {3}}}$, ${ displaystyle - { frac {1} {3}}}$, ${ weergavestijl { frac {1} {6}}}$, ${ displaystyle - { frac {1} {6}}}$, ${ weergavestijl 2}$, ${ weergavestijl -2}$, ${ weergavestijl { frac {2} {3}}}$ en ${ displaystyle - { frac {2} {3}}}$... De hele wortels van de derdegraadsvergelijking zijn enkele getallen uit deze lijst.
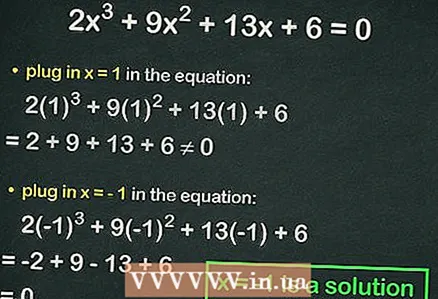4. 4 Vul gehele getallen in de derdegraadsvergelijking in. Als de gelijkheid waar is, is het gesubstitueerde getal de wortel van de vergelijking. Vervang bijvoorbeeld in de vergelijking ${ weergavestijl 1}$:
   • ${ displaystyle 2 (1) ^ {3} +9 (1) ^ {2} +13 (1) +6}$ = ${ weergavestijl 2 + 9 + 13 + 6}$ ≠ 0, dat wil zeggen dat er geen gelijkheid wordt waargenomen. Voer in dit geval het volgende nummer in.
   • Vervanging ${ weergavestijl -1}$: ${ weergavestijl (-2) +9 + (- 13) +6}$ = 0. Dus, ${ weergavestijl -1}$ is de hele wortel van de vergelijking.
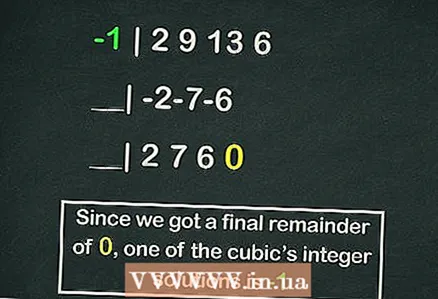5. 5 Gebruik de methode om polynomen te delen door Horner's schemaom de wortels van de vergelijking sneller te vinden. Doe dit als u getallen niet handmatig in de vergelijking wilt vervangen. In het schema van Horner worden gehele getallen gedeeld door de waarden van de coëfficiënten van de vergelijking ${ weergavestijl a}$, ${ weergavestijl b}$, ${ weergavestijl c}$ en ${ weergavestijl d}$... Als de getallen deelbaar zijn (dat wil zeggen, de rest is ${ weergavestijl 0}$), is een geheel getal de wortel van de vergelijking.
   • Het schema van Horner verdient een apart artikel, maar het volgende is een voorbeeld van het berekenen van een van de wortels van onze derdegraadsvergelijking met dit schema:

     -1 | 2 9 13 6

     __| -2-7-6

     __| 2 7 6 0

   • Dus de rest is ${ weergavestijl 0}$, maar ${ weergavestijl -1}$ is een van de wortels van de vergelijking.

Methode 3 van 3: Hoe een vergelijking op te lossen met behulp van de discriminant?

1. 1 Noteer de waarden van de coëfficiënten van de vergelijking een{ weergavestijl a}, B{ weergavestijl b}, C{ weergavestijl c} en NS{ weergavestijl d}. We raden u aan om vooraf de waarden van de aangegeven coëfficiënten op te schrijven om in de toekomst niet in de war te raken.
   • Bijvoorbeeld, gegeven de vergelijking ${ weergavestijl x ^ {3} -3x ^ {2} + 3x-1}$... Schrijf op ${ weergavestijl a = 1}$, ${ weergavestijl b = -3}$, ${ weergavestijl c = 3}$ en ${ weergavestijl d = -1}$... Bedenk dat indien eerder ${ weergavestijl x}$ er is geen getal, de bijbehorende coëfficiënt bestaat nog steeds en is gelijk aan ${ weergavestijl 1}$.
2. 2 Bereken de nuldiscriminant met een speciale formule. Om een ​​derdegraadsvergelijking met behulp van de discriminant op te lossen, moet u een aantal moeilijke berekeningen uitvoeren, maar als u alle stappen correct uitvoert, wordt deze methode onmisbaar voor het oplossen van de meest complexe derdegraadsvergelijkingen. Eerste berekening ${ displaystyle Delta _ {0}}$ (zero discriminant) is de eerste waarde die we nodig hebben; om dit te doen, vervangt u de overeenkomstige waarden in de formule ${ displaystyle Delta _ {0} = b ^ {2} -3ac}$.
   • De discriminant is een getal dat de wortels van een polynoom kenmerkt (de discriminant van een kwadratische vergelijking wordt bijvoorbeeld berekend met de formule ${ weergavestijl b ^ {2} -4ac}$).
   • In onze vergelijking:

     ${ displaystyle b ^ {2} -3ac}$

     ${ weergavestijl (-3) ^ {2} -3 (1) (3)}$

     ${ weergavestijl 9-3 (1) (3)}$

     ${ displaystyle 9-9 = 0 = Delta _ {0}}$

3. 3 Bereken de eerste discriminant met behulp van de formule Δ1=2B3−9eenBC+27een2NS{ displaystyle Delta _ {1} = 2b ^ {3} -9abc + 27a ^ {2} d}. Eerste discriminant ${ displaystyle Delta _ {1}}$ - dit is de tweede belangrijke waarde; om het te berekenen, sluit u de bijbehorende waarden in de opgegeven formule aan.
   • In onze vergelijking:

     ${ displaystyle 2 (-3) ^ {3} -9 (1) (- 3) (3) +27 (1) ^ {2} (- 1)}$

     ${ weergavestijl 2 (-27) -9 (-9) +27 (-1)}$

     ${ weergavestijl -54 + 81-27}$

     ${ displaystyle 81-81 = 0 = Delta _ {1}}$

4. 4 Berekenen:${ displaystyle Delta = ( Delta _ {1} ^ {2} -4 Delta _ {0} ^ {3}) div -27a ^ {2}}$... Dat wil zeggen, vind de discriminant van de derdegraadsvergelijking via de verkregen waarden ${ displaystyle Delta _ {0}}$ en ${ displaystyle Delta _ {1}}$... Als de discriminant van een derdegraadsvergelijking positief is, heeft de vergelijking drie wortels; als de discriminant nul is, heeft de vergelijking een of twee wortels; als de discriminant negatief is, heeft de vergelijking één wortel.
   • Een derdegraadsvergelijking heeft altijd ten minste één wortel, aangezien de grafiek van deze vergelijking de X-as op ten minste één punt snijdt.
   • In onze vergelijking ${ displaystyle Delta _ {0}}$ en ${ displaystyle Delta _ {1}}$ zijn gelijk ${ weergavestijl 0}$, zodat u gemakkelijk kunt berekenen ${ weergavestijl Delta}$:

     ${ displaystyle ( Delta _ {1} ^ {2} -4 Delta _ {0} ^ {3}) div (-27a ^ {2})}$

     ${ displaystyle ((0) ^ {2} -4 (0) ^ {3}) div (-27 (1) ^ {2})}$

     ${ weergavestijl 0-0 div 27}$

     ${ weergavestijl 0 = Delta}$... Onze vergelijking heeft dus een of twee wortels.

5. 5 Berekenen:${ displaystyle C = ^ {3} { sqrt { left ({ sqrt { Delta _ {1} ^ {2} -4 Delta _ {0} ^ {3}}} + Delta _ {1 } rechts) div 2}}}$. ${ weergavestijl C}$ - dit is de laatste belangrijke hoeveelheid die gevonden kan worden; het zal je helpen de wortels van de vergelijking te berekenen. Vervang de waarden in de opgegeven formule ${ displaystyle Delta _ {1}}$ en ${ displaystyle Delta _ {0}}$.
   • In onze vergelijking:

     ${ displaystyle ^ {3} { sqrt {{ sqrt {( Delta _ {1} ^ {2} -4 Delta _ {0} ^ {3}) + Delta _ {1}}} div 2}}}$

     ${ displaystyle ^ {3} { sqrt {{ sqrt {(0 ^ {2} -4 (0) ^ {3}) + (0)}} div 2}}}$

     ${ displaystyle ^ {3} { sqrt {{ sqrt {(0-0) +0}} div 2}}}$

     ${ weergavestijl 0 = C}$

6. 6 Zoek drie wortels van de vergelijking. Doe het met de formule ${ displaystyle - (b + u ^ {n} C + Delta _ {0} div (u ^ {n} C)) div 3a}$, waar ${ displaystyle u = (- 1 + { sqrt {-3}}) div 2}$, maar N is gelijk aan 1, 2 of 3... Vervang de juiste waarden in deze formule - als resultaat krijgt u drie wortels van de vergelijking.
   • Bereken de waarde met de formule at N = 1, 2 of 3en controleer vervolgens het antwoord. Als u 0 krijgt wanneer u uw antwoord controleert, is deze waarde de wortel van de vergelijking.
   • Vervang in ons voorbeeld 1 in ${ weergavestijl x ^ {3} -3x ^ {2} + 3x-1}$ en krijg 0, d.w.z 1 is een van de wortels van de vergelijking.